[알고리즘 정리] 최장 공통 부분 수열(LCS)
Logest Common Subequence
우리 말로 최장 공통 부분 수열이라고도 불리는 알고리즘이다. 어떤 문자열이 두 개 있을 때, 두 수열 사이에 있는 공통적인 문자들의 가장 긴 조합을 찾는 문제이다. 예를 들어 다음 두 문자열이 있다고 하자.
Y = (B, D, C, A, B, A)
두 문자열의 사이에는 많은 부분 문자열들이 있는데, 문자가 하나 뿐인 부분 문자열을 제외하고 모두 나열해보면 다음과 같다:
A, B, A
B, C
B, C, B
C, B
C, B, A
B, D
B, D, A
B, D, A, B
이 중에서 가장긴 부분 문자열은 B,D,A,B가 될 것이다.
Brute-Force
이 문제를 해결하기 위해서 먼저 브루트 포스로 모든 경우의 수를 따져보는 것을 고려해보자. 우리에게 두 개의 문자열 X[1...m] 과 Y[1...n] 가 있다고 해보자. 모든 경우의 수를 다 시도해보려면, X에 있는 모든 부분 문자열을 구해서 Y에 대입해보면 된다. 따라서 브루트 포스로 이 문제를 해결하는 속도는,
- m 개의 문자로 이루어진 문자열 X에서 모든 부분 문자열을 만들 때 걸리는 속도 2m.
- 위에서 구한 부분수열을 Y에 대입해볼 때 소요되는 속도 O(n).
두 연산 시간의 합이 되고 최악의 경우를 고려했을 때, O(n2m) 으로 표현할 수 있다. 따라서 m의 갯수에 따라 엄청난 시간이 걸릴 수 있기 때문에 브루트 포스는 이 문제를 해결하는데 적합한 접근이 아니다.
Dynamic Programming
Step 1 : Optimal Substructure
문제를 일반화하기 위해서 비교해야하는 문자열을 X=<x1, x2, ... , xm>, Y=<y1, y2, ... , yn> 라고 하고, 두 문자열의 LCS를 Z=<z1, z2, ... , zk> 라고 해보자. 그렇다면 우리는 다음과 같은 명제가 성립한다고 할 수 있을 것이다.
- xm = yn 이라면, xm = yn = zk 이고 새로운 LCS 는 Xm-1 와 Yn-1 이라고 할 수 있다.
- 수식이 헷갈릴 수도 있는데, 매우 당연한 이야기를 수학적으로 표현한 것이다. 두 문자열의 가장 끝 문자가 서로 같다면, LCS의 가장 끝이 해당 문자로 끝나는 것은 너무나 자명하지 않은가?
- xm ≠ yn 이라면, xm ≠ zk 이고 새로운 LCS 는 Xm-1 와 Y 이라고 할 수 있다.
- xm ≠ yn 이라면, yn ≠ zk 이고 새로운 LCS 는 X 와 Yn-1 이라고 할 수 있다.
- 만약 두 문자가 다르다고 한다면, 우리는 두 가지 경우를 생각할 수 있다. X 문자열의 길이를 줄이거나, Y 문자열의 길이를 줄이는 것이다.
우리가 구하고자 하는 것은 가장 긴 부분 문자열을 구성하게되는 조합이기 때문에 두 경우 중에서 더 큰 부분 문자열을 만드는 쪽을 선택해야 할 것이다.
Step 2 : Recursive Solution
위 논리가 꽤나 타당하고 생각이 든다. 그렇다면 수식으로 만들어보자.
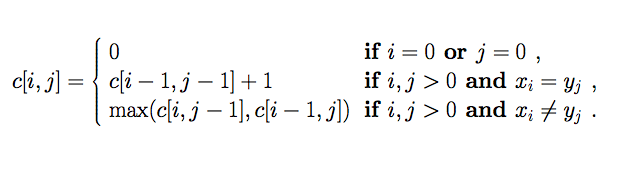
c[i, j] 가 i, j 사이의 최대 부분 문자열의 길이를 가지고 있다고 한다면, X 와 Y 의 문자가 같을 때, 바로 이전 최장 문자열의 길이에 1을 더한 값을 새로 저장하고, 두 문자가 다를 때는 X쪽 최장 문자열의 길이와 Y쪽 최장 문자열의 길이를 비교해서 더 큰 값을 가져온다.
그런데 위 계산식 대로 진행하면, 우리는 결국 똑같은 연산을 계속해서 해야하는 상황을 맞이한다. 그리고 이런 상황은 연산 시간을 낭비하게 한다. 따라서 우리는 한번 계산한 결과를 테이블에 저장해두고 재사용하는 방식을 시도해야한다.
Step 3 : Computing the Optimal Costs
이미 계산한 값을 재사용하기 위해서 2차원 배열을 통해 테이블을 만들어 이 문제를 풀어보자.
| Y\X | 0 | A | B | C | B | D | A | B |
|---|---|---|---|---|---|---|---|---|
| 0 | ||||||||
| B | ||||||||
| D | ||||||||
| C | ||||||||
| A | ||||||||
| B | ||||||||
| A |
위와 같이 테이블을 세팅하자. 그리고 모든 X의 문자에 대해서 Y의 문자를 꺼내와 비교해서 위에서 작성했던 수식에 따라 값을 채워 넣자. 첫 몇 개를 진행해보면,
| Y\X | 0 | A | B | C | B | D | A | B |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| B | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 0 | |||||||
| C | 0 | |||||||
| A | 0 | |||||||
| B | 0 | |||||||
| A | 0 |
B에 대한 행은 다음과 같이 채울 수 있다. A를 만났을 때는 이전 값 중에 제일 큰 0을 넣어주었다. 그리고 B를 만나게 되면 Xi 와 Yj 의 값이 같기 때문에 이전 위치의 가장 긴 길이인 0에 1을 더해 1로 채워주고 있다. C를 체크해보면 B와 C는 다른 값이기 때문에, X를 제외 했을 때, 즉 바로 왼쪽에 있는 값과, Y를 제외했을 때, 즉 좌측 대각선 위에 있는 값 중에 더 큰 값으로 배열을 채워주게 된다. 이 논리대로 테이블을 모두 채워나가면 다음과 같이 표를 완성시킬 수 있다.
| Y\X | 0 | A | B | C | B | D | A | B |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| B | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| D | 0 | 0 | 1 | 1 | 1 | 2 | 2 | 2 |
| C | 0 | 0 | 1 | 2 | 2 | 2 | 2 | 2 |
| A | 0 | 1 | 1 | 2 | 2 | 2 | 3 | 3 |
| B | 0 | 1 | 2 | 2 | 3 | 3 | 3 | 4 |
| A | 0 | 1 | 2 | 2 | 3 | 3 | 4 | 4 |
위 표에서 확인할 수 있는 것 처럼 우리가 얻을 수 있는 LCS의 길이는 4이고, 해당 길이로 조합할 수 있는 부분 문자열은 총 3종류가 된다. 왜냐하면 LCS는 여러개가 나올 수 있고 표에서 최대 값을 가지는 아이템의 갯수가 그 경우의 수를 의미하기 때문이다. 위와 같은 알고리즘으로 계산을 진행하게 되면, 우리는 LCS를 단순히 표의 모든 위치를 순회하는 것을 통해 알 수 있기 때문에, 연산 속도는 𝛩(mn) 으로 표현할 수 있다.
위 표를 기준으로 LCS인 서브스트링을 얻으려면 LCS 값을 가지고 있는 아이템 위치부터 왼쪽으로 이동하면서, X와 Y가 같은 알파벳들을 기록해주면 된다. 여러 문자열이 나올 수 있지만 하나를 예로 들어보면, B -> A -> D -> B 의 역순으로 나열한 문자열인 BDAB 가 하나의 LCS가 될 것이다.
Step 4: Constructing an Optimal Solution
이제 코드로 구현해보자. LCS 문제는 꽤나 유명한 문제이기 때문에 [백준 알고리즘] 알고리즘에서 문제를 풀어볼 수 있었다.
문제: https://www.acmicpc.net/problem/9251
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
int dp[1001][1001];
int main()
{
string s1, s2;
cin >> s1 >> s2;
int lcs = 0;
for (int i = 1; i <= s2.size(); i++)
{
for (int j = 1; j <= s1.size(); j++)
{
dp[i][j] = dp[i - 1][j];
if (s2[i - 1] == s1[j - 1])
{
dp[i][j] = dp[i - 1][j - 1] + 1;
lcs = max(lcs, dp[i][j]);
}
else
{
if (dp[i - 1][j] > dp[i][j - 1])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = dp[i][j - 1];
}
}
}
cout << lcs;
return 0;
}'🔮 씨-에스 > 🗝 알고리즘' 카테고리의 다른 글
| [알고리즘 정리] 배낭 문제(Knapsack Problem) (7) | 2021.07.17 |
|---|---|
| [알고리즘 정리] 허프만 코드(Huffman Code Problem) (0) | 2021.07.17 |
| [알고리즘 정리] 그리디 알고리즘(Greedy Alogorithm) (0) | 2021.07.17 |
| [알고리즘 정리] 행렬 곱셈 문제 (Matrix Chain Multiplication) (0) | 2021.07.17 |
| [알고리즘 정리] 최장 증가 부분 수열(LIS) (0) | 2021.07.17 |